A Simple Guide to Subgradient
Contents
Definition
If $f(x)$ is a convex function, then the set $\partial f = \{v | f(x) \ge f(x _0) + v^T (x - x _0)\}$ is called the sub-gradient of $f(x)$ at the point of $x _0$. Here $v$ should be limited to a small neighborhood of $x _0$. Note that $v^T (x- x _0)$ can be a generalized inner product in some Banach space other than Euclidean space.
It is apparent that, if $f(x)$ is differentiable at $x _0$, then by definition $$f(x) - f(x _0) = f’(x _0) ^T (x - x _0) + o(\| x - x _0 \|) \ge v^T (x - x_0)$$. In this case, we can say that the sub-gradient of $f(x)$ at $x _0$ is exactly the gradient $f’(x _0)$. For non-differentiable points, the sub-gradient should be a set.
Geometric Explanation
Recall that, for unary functions, the derivative of $f(x)$ is the slope of the line lying exactly below the curve of $y = f(x)$ and tangent to the curve at $x _0$. Similarly, the subgradient corresponds to the lines lying below the function curve and $x _0$ is a intersection. Just like what P1 shows. When $f(x)$ is differentiable at $x _0$, such lines will merge into one, and that is the tangent line.
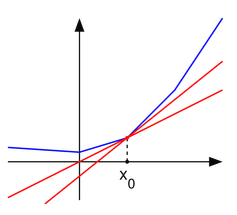
P1. The slopes of these lines are subgradients.
Take the absolute function as an example. By definition, its subgradient at $x = 0$ is $\{v | \|x\| \ge vx\}$. The solution of the inequality is $[-1, 1]$. The two endpoints are exactly the slopes of the curve when $x < 0$ and when $x > 0$.
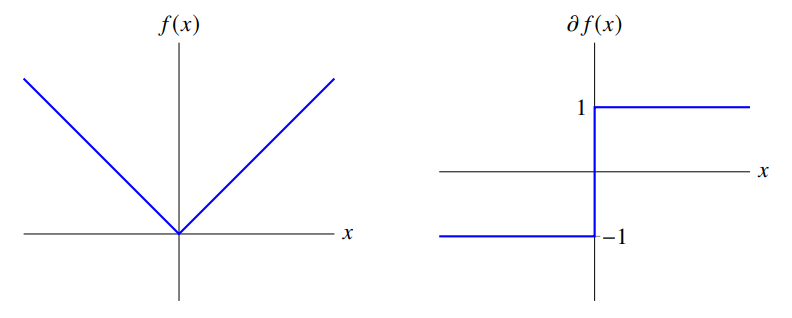
In Machine Learning, the $\ell _1$ regularization term is frequently used while it’s not differentiable at $x = 0$. However, we can still get the subgradient, which looks the same as the absolute function $\{v |\ \| x \|\ge v^T x \}$ and the solution is $\| v\|\le 1$.
Application
The purpose of introducing subgradient in optimization is that we can derive a necessary condition for non-smooth functions to attain minima and maxima.
Theorem: If $f(x)$ is a convex function and there exists a subgradient within a neighborhood of $x _0$, then $x _0$ is a extrema of $f(x)$ if $0 \in \partial f(x _0)$.
For differentiable functions, a necessary condition for an extremum is that the slope of the tangent line is 0 (Fermat’s Theorem). So considering the geometric meaning of subgradient, this theorem indicates that there exists such a horizontal line that it is under the curve and intersect at $x _0$.
Similarly, we can modify the KKT condition from $\nabla \mathcal L (x, \lambda) = 0$ to $0 \in \partial \mathcal L (x, \lambda)$. Therefore, subgradient becomes really useful when it comes to solving the optimization problems of some non-differentiable target functions like $\ell _1$ norm.